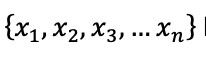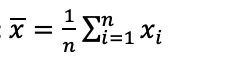Escrito por proesusertd
La media aritmética es el valor promedio de un conjunto de datos numéricos, calculada como la suma del conjunto de valores dividida entre el número total de valores. A menudo se conoce también como promedio. Es una medida de tendencia central junto a otras como la moda, la mediana u otros conceptos de media como la media geométrica, ponderada, etc. que no cubriremos aquí.
Sea nuestro conjunto de datos el siguiente:
la media se formula de la siguiente forma:
Veamos la media en un ejemplo más fácil.
Ejemplo A: Estatura clase de primaria
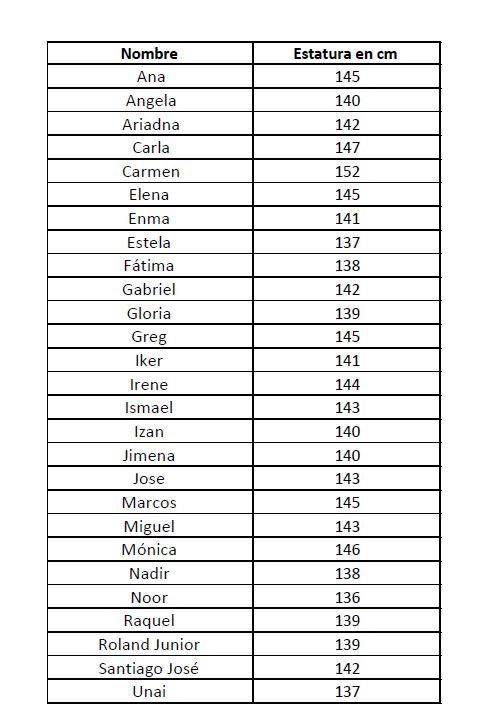
En una clase de 5º de primaria han hecho el siguiente ejercicio: medirse en centímetros todos los alumnos obteniendo la siguiente tabla de datos:
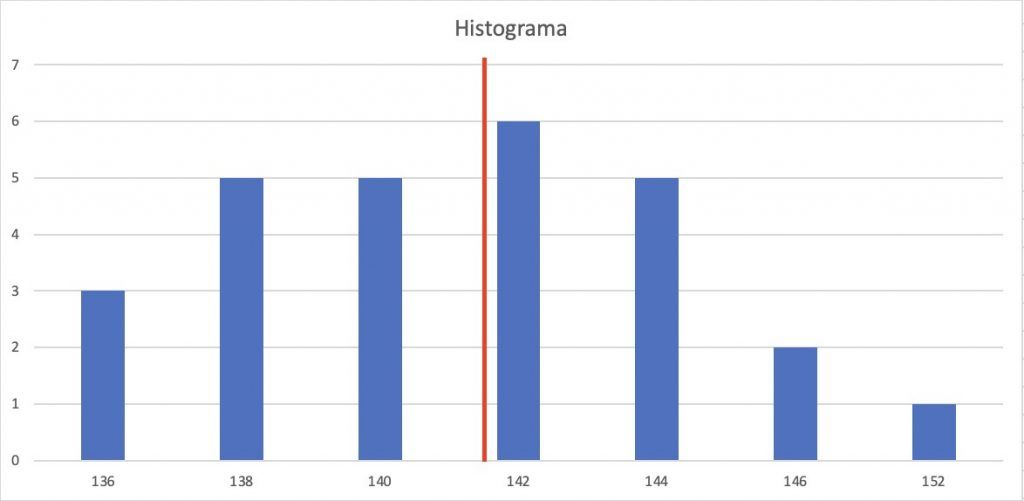
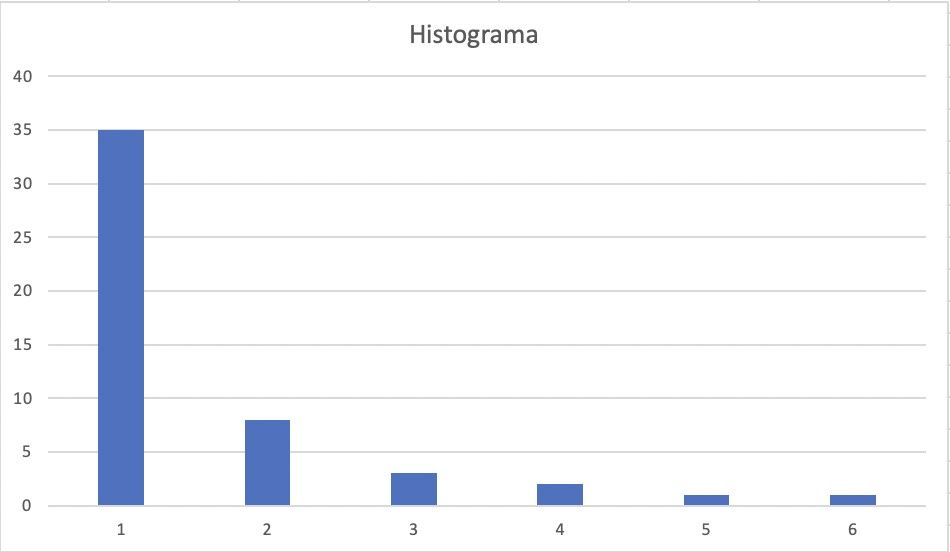
La media de altura de esta clase, calculada según la fórmula, sumando todas las alturas y dividirla entre el total de alumnos: 22, redondeada a 2 decimales es de 141,81 cm. Agrupamos las mediciones en rangos de 2 cms y mostramos los datos en forma de barras vemos el histograma de esta muestra. Incluimos en rojo donde se posiciona la media calculada:
Nos aparecen los casos más recurrentes alrededor de la media, en nuestra mente todo cuadra bien según nuestra intuición estadística. Este concepto lo tenemos muy arraigado aunque nos lleva a cometer sesgos en la intuición estadística que de adultos muy formados y sesudos cometemos con facilidad. En nuestra mente tenemos detrás distribuciones normales, “campanas de Gauss” donde las colas son conocidas y muy improbables. Esa pasta la tenemos muy interiorizada y nos conlleva a cometer errores de entendimiento, que a veces conllevan decisiones, que pagamos caras.
Veamos otros dos ejemplos también muy cotidianos que cuestionan la media como ese simple indicador válido para una población que como hemos dicho todos llevamos grabado a fuego.
Ejemplo B: Tiempos de servicio entrega de paquetería
Imaginemos una compañía de reparto de paquetería de “última milla”. Son aquellos que nos llevan el paquete a nuestra casa. Reciben los paquetes de su central una vez al día y su labor es la entrega al cliente. La central les exige que “los envíos deben quedar hechos en media en el día, los que entrega rápidos en la mañana por los que entregue más tarde o el día siguiente”.
El operador diligente anota sus tiempos de entrega para el primer lote de 50 envíos que sí consiguió entregar y que recibe a las 8 de la mañana un lunes. A las 9 tiene la ruta preparada y va anotando en horas naturales desde las 8 de la mañana que firmó la recepción. La tabla es la siguiente:
| Pedido | Horas | Dia |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 1 |
| 4 | 1 | 1 |
| 5 | 1 | 1 |
| 6 | 2 | 1 |
| 7 | 2 | 1 |
| 8 | 2 | 1 |
| 9 | 2 | 1 |
| 10 | 3 | 1 |
| 11 | 3 | 1 |
| 12 | 3 | 1 |
| 13 | 3 | 1 |
| 14 | 4 | 1 |
| 15 | 4 | 1 |
| 16 | 4 | 1 |
| 17 | 4 | 1 |
| 18 | 5 | 1 |
| 19 | 5 | 1 |
| 20 | 5 | 1 |
| 21 | 7 | 1 |
| 22 | 7 | 1 |
| 23 | 7 | 1 |
| 24 | 8 | 1 |
| 25 | 8 | 1 |
| 26 | 8 | 1 |
| 27 | 8 | 1 |
| 28 | 9 | 1 |
| 29 | 9 | 1 |
| 30 | 9 | 1 |
| 31 | 9 | 1 |
| 32 | 10 | 1 |
| 33 | 10 | 1 |
| 34 | 23 | 1 |
| 35 | 23 | 1 |
| 36 | 24 | 2 |
| 37 | 25 | 2 |
| 38 | 26 | 2 |
| 39 | 27 | 2 |
| 40 | 28 | 2 |
| 41 | 29 | 2 |
| 42 | 30 | 2 |
| 43 | 32 | 2 |
| 44 | 50 | 3 |
| 45 | 53 | 3 |
| 46 | 56 | 3 |
| 47 | 78 | 4 |
| 48 | 82 | 4 |
| 49 | 96 | 5 |
| 50 | 123 | 6 |
Le dicen desde la central que la media de este servicio es de 19,36h que sumadas a las 8 de la mañana que recibió la mercancía significa que no ha cumplido el objetivo. Sin embargo… ¿es representativo del servicio prestado? ¡Entregó el 70% de los envíos en el mismo día!. La media NO es un buen indicador en este análisis, hay otros indicadores estándar de servicio que sirven mucho mejor para medir este tipo de información. Como se puede observar, no tenemos distribución normal.
Ejemplo C: La renta familiar en el Bernabeu
Este es más radical y muy conocido, hay muchas versiones del mismo. Imaginemos que supiéramos la renta familiar de todos los asistentes a un partido de fútbol en el Bernabéu. Alguien diría, saquemos la media para conocer la renta tipo por asistente. Según el INE la renta familiar media en Madrid es de 35.587 EUR, debería salirnos algo parecido en el ejercicio. Pero sin embargo… imaginemos que ese día Florentino invitó a su amigo Amancio Ortega y que éste viene con su hija. Al añadir esos tres individuos la media se moverá, algo que no ocurrirá si añadimos otros 300 aficionados estándar repartidos por la geografía de Madrid. Apenas 3 elementos, han movido la media. ¿Y si fuera Jezz Bezos?
La media sufre mucho por las mediciones extremas a priori poco probables en una distribución normal de un ejercicio teórico… sin embargo el mundo real, pocas veces es “normal”. Es importante conocer cómo se distribuye nuestra variable y aplicar el mejor indicador para conocer la población y es importante romper con los pensamientos rápidos e intuitivos que están simplificando el análisis, seguramente contra una distribución normal.
Imagen de portada de Freepik <a href=»https://www.freepik.es/fotos/patron»>Foto de Patrón creado por jcomp – www.freepik.es</a>
¿Quieres recibir artículos como éste en tu correo?
¿Te ha gustado este análisis y quieres recibir más como éste? Suscríbete a nuestra newsletter y te enterarás en el momento de publicarlo.